Functions and iterations

Seong-Hwan Jun

2025-09-25

Spot a bug

df <- tibble(
  a = rnorm(5),
  b = rnorm(5),
  c = rnorm(5),
  d = rnorm(5),
)

df |> mutate(
  a = (a - min(a, na.rm = TRUE)) / 
    (max(a, na.rm = TRUE) - min(a, na.rm = TRUE)),
  b = (b - min(a, na.rm = TRUE)) / 
    (max(b, na.rm = TRUE) - min(b, na.rm = TRUE)),
  c = (c - min(c, na.rm = TRUE)) / 
    (max(c, na.rm = TRUE) - min(c, na.rm = TRUE)),
  d = (d - min(d, na.rm = TRUE)) / 
    (max(d, na.rm = TRUE) - min(d, na.rm = TRUE)),
)

Functions improve resuability

normalize <- function(x) {
  (x - min(x, na.rm = TRUE)) / 
    (max(x, na.rm = TRUE) - min(x, na.rm = TRUE))
}

df |> mutate(
  a = normalize(a),
  b = normalize(b),
  c = normalize(c),
  d = normalize(d),
)

# A tibble: 5 × 4
      a     b     c     d
  <dbl> <dbl> <dbl> <dbl>
1 0.564 0.161 0.208 0.391
2 0     0.215 0.253 0.723
3 0.231 0.327 1     1    
4 0.299 1     0     0.524
5 1     0     0.222 0

Function syntax

function_name <- function(arg1, arg2, ...) {
  # function body
  # ...
  return(value)  # optional
}

Benefits of functions

Choose an evocative name that makes your code easier to understand.
As requirements change, you only need to update code in one place, instead of many.
You eliminate the chance of making incidental mistakes when you copy and paste (i.e. updating a variable name in one place, but not in another).
It makes it easier to reuse work from project-to-project, increasing your productivity over time.

Exercise I: improve `normalize`

Normalize based on user specified quantiles instead of min and max.

normalize <- function(x, probs) {
  rng <- quantile(x, probs = probs, na.rm = TRUE)
  (x - rng[1]) / (rng[2] - rng[1])
}

Exercise II: improve `normalize`

This new function breaks the existing code:

df |> mutate(
  a = normalize(a),
  b = normalize(b),
  c = normalize(c),
  d = normalize(d),
)

Error in `mutate()`:
ℹ In argument: `a = normalize(a)`.
Caused by error in `normalize()`:
! argument "probs" is missing, with no default

How to fix it?

Exercise II: improve `normalize`

We can add a default value so that legacy code (existing users of the function) doesn’t break.

normalize <- function(x, probs=c(0,1)) {
  rng <- quantile(x, probs = probs, na.rm = TRUE)
  (x - rng[1]) / (rng[2] - rng[1])
}

df |> mutate(
  a = normalize(a),
  b = normalize(b),
  c = normalize(c),
  d = normalize(d),
)

# A tibble: 5 × 4
      a     b     c     d
  <dbl> <dbl> <dbl> <dbl>
1 0.564 0.161 0.208 0.391
2 0     0.215 0.253 0.723
3 0.231 0.327 1     1    
4 0.299 1     0     0.524
5 1     0     0.222 0

Higher-order functions

Functions that take other functions as arguments or return functions as their result.

base::apply function signature:

apply <- function (X, MARGIN, FUN, ..., simplify = TRUE)
# ...  
}

X is an array (matrix)
MARGIN indicates whether the function will be applied over 1: rows or 2: columns.
FUN is a function to be applied.

Function as an argument

mat <- matrix(1:9, nrow=3)
apply(mat, 1, mean)  # row means

[1] 4 5 6

apply(mat, 2, mean)  # column means

[1] 2 5 8

…

... (dot-dot-dot) is a special argument, “catch-all”, that allows you to pass a variable number of arguments to a function.

mat <- matrix(1:9, nrow=3)
diag(mat) <- NA
apply(mat, 1, mean, na.rm = TRUE)  # row means

[1] 5.5 5.0 4.5

apply(mat, 2, mean, na.rm = TRUE)  # column means

[1] 2.5 5.0 7.5

na.rm is an argument to mean function, not apply.

`optim` the great

optim(par, fn, gr = NULL, ...,
      method = c("Nelder-Mead", "BFGS", "CG", "L-BFGS-B", "SANN",
                 "Brent"),
      lower = -Inf, upper = Inf,
      control = list(), hessian = FALSE)

par: initial values for the parameters to be optimized.
fn: the function to be minimized.
gr: a function to compute the gradient of fn. If NULL, the gradient is approximated numerically.
...: arguments to be passed to fn and gr.

`optim` the great

m <- 1
s <- 3
log_gaussian_pdf <- function(x, mu, sd) {
  -dnorm(x, mean = mu, sd = sd, log = TRUE)
}
results <- optim(0, log_gaussian_pdf, mu = m, sd = s, method="Brent", lower=-100, upper=100)
results$par

[1] 0.9999999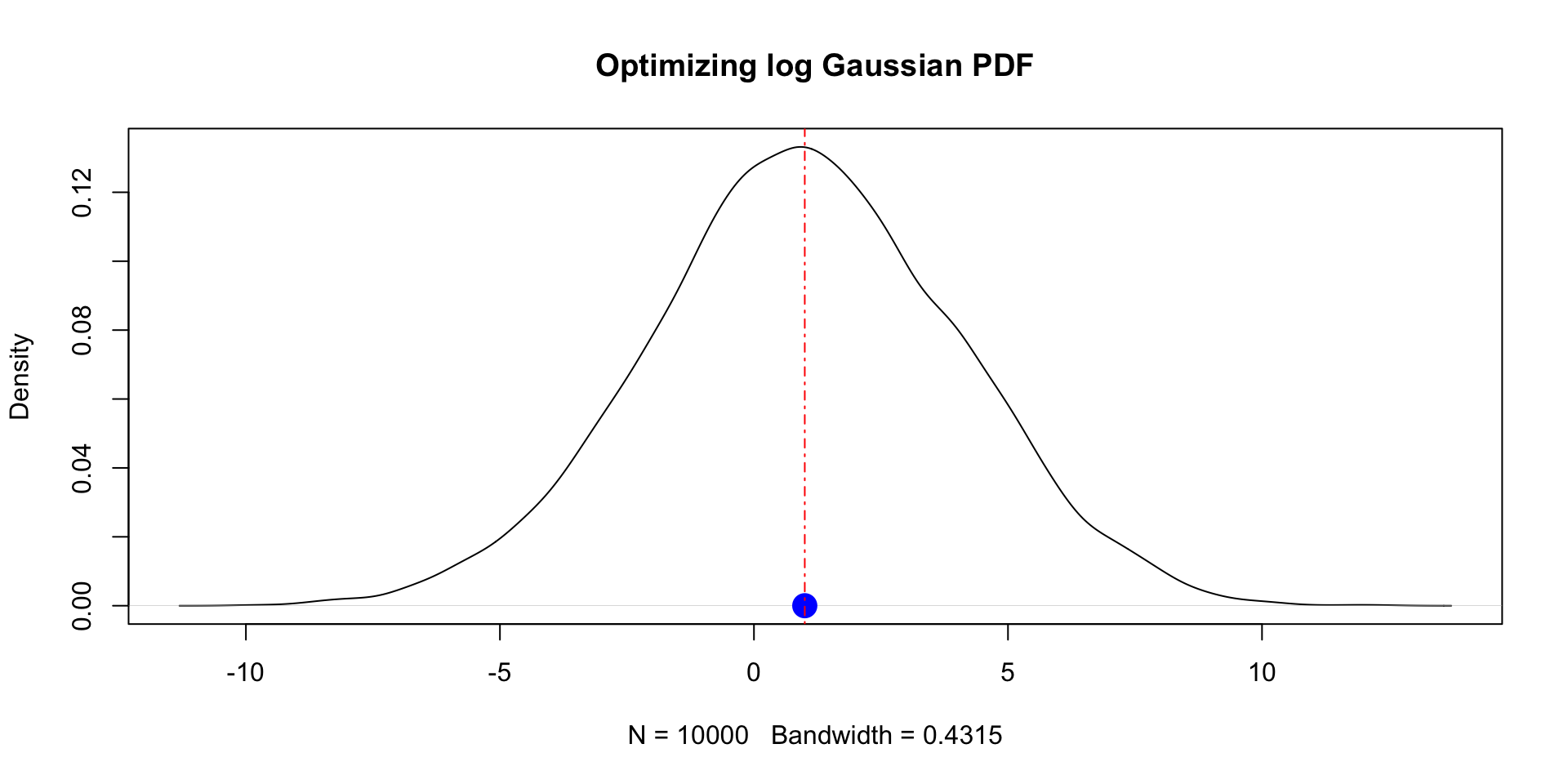

`optim` the great

Many uses:

find maximum likelihood estimates or find posterior mode.
minimize cost or loss functions (sum of square).
can work with multivariate functions.

lambdas: anonymous functions

Some functions are needed only in a specific context and serve no further use.

apply(mat, 1, function(x) x^2 + x - 3)

     [,1] [,2] [,3]
[1,]   NA    3    9
[2,]   17   NA   39
[3,]   53   69   NA

If function x^2 + x + 3 is used once and never really again, we can define it inline without naming it.

Recursive functions

Function can call itself.

fib <- function(n) {
  if (n <= 1) {
    return(n)
  } else {
    return(fib(n - 1) + fib(n - 2))
  }
}

What does this function do?

Recursive functions

fib(1)

[1] 1

fib(2)

[1] 1

fib(3)

[1] 2

fib(4)

[1] 3

fib(5)

[1] 5

fib(6)

[1] 8

fib(7)

[1] 13

Components of a recursive function

Recursive functions are useful when for breaking down complex problem into simpler ones.

Base Case: The condition that stops the recursion (e.g., if (n <= 1)). Without it, the function would call itself forever.
Recursive Step: The part where the function calls itself (e.g., fib(n - 1) + fib(n - 2)).
Recursion can be slow or even cause R to crash with a “stack overflow” error. This is because each function call uses a bit of memory, and too many nested calls can exhaust it.

Nested (or inner) function

foo <- function(x)
{
  bar <- function(y) {
    y^2 + 1 + x
  }
  bar(3)
}
foo(2)

What is the output of foo(2)?

Function factories

foo <- function(x)
{
  bar <- function(y) {
    return(x^y)
  }
  return(bar)
}
f <- foo(2)
f(3)

What is the output of f(3)?

Function indirection: `get`

f <- get("mean")
f(c(1, 3, 5, 7))

What will be the output?

Function indirection: `do.call`

do.call(what, args, quote = FALSE, envir = parent.frame())

what: a function or a string naming the function to be called.
args: a list of arguments to be passed to the function.

compute_stat <- function(func, args) {
  do.call(func, args)
}
compute_stat(mean, list(c(1, 3, 5, 7, 15, NA), na.rm=TRUE))
compute_stat(median, list(c(1, 3, 5, 7, 15, NA), na.rm=TRUE))
compute_stat(function(x) sum(x^2), list(c(1, 3, 5, 7, 15)))

Function indirection: tidyverse

Programming with Tidyverse: use double curly braces { }.

set.seed(123)
df <- tribble(
  ~group, ~number,
  "A", rnorm(1, mean = -5, sd = 1),
  "A", rnorm(1, mean = -5, sd = 1),
  "A", rnorm(1, mean = -5, sd = 1),
  "B", rnorm(1, mean = 10, sd = 1),
  "B", rnorm(1, mean = 10, sd = 1),
)
df

# A tibble: 5 × 2
  group number
  <chr>  <dbl>
1 A      -5.56
2 A      -5.23
3 A      -3.44
4 B      10.1 
5 B      10.1

Function indirection: tidyverse

compute_stat <- function(df, group_var, stat_var, func) {
  df |> group_by({{ group_var }}) |> summarise(stat = func({{ stat_var }}, na.rm=TRUE))
}
compute_stat(df, group, number, mean)

# A tibble: 2 × 2
  group  stat
  <chr> <dbl>
1 A     -4.74
2 B     10.1

compute_stat(df, group, number, sum)

# A tibble: 2 × 2
  group  stat
  <chr> <dbl>
1 A     -14.2
2 B      20.2

Function scope

Variables defined inside a function are local to that function.

foo <- function(x) {
  a <- 3
  y <- x^a
  return(y)
}
a # Results in an error

Error: object 'a' not found

Function scope

increment_counter <- function(x) {
  # 'counter' is created fresh every time the function is called
  counter <- 0
  counter <- counter + 1
  return(x + counter)
}
increment_counter(10)

[1] 11

increment_counter(20)

[1] 21

No state persists across function calls.

Function scope: super assignment operator `<<-`

make_counter <- function() {
  # 1. A variable is created in the parent environment
  count <- 0 
  # 2. The factory returns a new, inner function
  inner_function <- function() {
    # 3. Use the super-assignment operator '<<-'
    # This modifies 'count' in the parent environment, not locally.
    count <<- count + 1#<<
    return(count)
  }
  return(inner_function)
}

Function scope: closure

counter_a <- make_counter()
counter_a()

[1] 1

counter_a()

[1] 2

counter_a()

[1] 3

Inner function maintains the state even after parent function terminates.

Function scope: global environment

# Define 'a' in the global environment
a <- 10

bar <- function(x) {
  # 'a' is not defined inside 'bar', so R looks outside
  # and finds the global 'a' we just defined.
  y <- x + a
  return(y)
}

# The function works by using the global variable
bar(5)

[1] 15

Iteration: for-loop

for (variable in set) {
  # code to be executed
}

for (i in 1:5) {
  print(i^2)
}

[1] 1
[1] 4
[1] 9
[1] 16
[1] 25

Iteration: while-loop

while (condition) {
  # code to be executed
}

counter_b <- make_counter()
x <- counter_b()
while (x < 5) {
  x <- counter_b()
}

Iteration: repeat-loop

repeat {
  # code to be executed
  if (condition) {
    break
  }
}

counter_c <- make_counter()
repeat {
  y <- counter_c()
  if (y < 7) {
    break
  }
}

Vectorized operations

Loops. R has to interpret each step of the loop one by one: check the condition, assign the value, increment the counter, and repeat. This involves a lot of overhead.
Vectorized calls. R hands off the entire operation to highly optimized, pre-compiled code written in a lower-level language like C or Fortran. This code runs much closer to the machine level and executes the entire task in one efficient go.

Vectorized operations

num_samples <- 100000
time_loop <- system.time({
  x <- numeric(num_samples)
  for (n in 1:num_samples) {
    x[n] <- rnorm(1) # Corrected from x[i] and specified rnorm(1)
  }
})
time_vectorized <- system.time({
  y <- rnorm(num_samples)
})
print(time_loop) # Loop time

   user  system elapsed 
  0.209   0.047   0.262

print(time_vectorized) # Vectorized time

   user  system elapsed 
  0.006   0.000   0.006

Testing with `testthat`

Once you implement your function, you may want to verify that it works as expected.
The main package for testing is testthat https://testthat.r-lib.org/.
testthat offers various convenient functions to check if your function behaves as expected.

library(testthat)
test_that("Fibonacci test", {
  expect_equal(fib(1), 1)
  expect_equal(fib(2), 1)
  expect_equal(fib(7), 13)
})

Test passed 😸

Functions and iterations

Spot a bug

Functions improve resuability

Function syntax

Benefits of functions

Exercise I: improve normalize

Exercise II: improve normalize

Exercise II: improve normalize

Higher-order functions

Function as an argument

…

optim the great

optim the great

optim the great

lambdas: anonymous functions

Recursive functions

Recursive functions

Components of a recursive function

Nested (or inner) function

Function factories

Function indirection: get

Function indirection: do.call

Function indirection: tidyverse

Function indirection: tidyverse

Function scope

Function scope

Function scope: super assignment operator <<-

Function scope: closure

Function scope: global environment

Iteration: for-loop

Iteration: while-loop

Iteration: repeat-loop

Vectorized operations

Vectorized operations

Testing with testthat

Exercise I: improve `normalize`

Exercise II: improve `normalize`

Exercise II: improve `normalize`

`optim` the great

`optim` the great

`optim` the great

Function indirection: `get`

Function indirection: `do.call`

Function scope: super assignment operator `<<-`

Testing with `testthat`