BST430 Lecture 11A

Functional programming with purrr

Seong-Hwan Jun

Map and reduce

Mapping: distribute a large scale data problem into smaller pieces and assign each piece to a different computing node.

Reduce: combine the results from each node into a final result.

Map and reduce

Example: count the frequency of words in a large corpus.

Each node counts the frequency of words in its assigned piece of the corpus (map).

Then, the counts from each node are combined to get the total counts (reduce).

Hadoop and Spark are widely used platforms for distributed computing that implement the MapReduce paradigm.

Map: functional

  • Essentially, map is a verb for applying a function to each element of a list or vector.
  • In R, base::apply is a basic example of map that applies a function to the margins of an array or matrix.
  • base::lapply function returns lists (hence the “l” in lapply).
  • The purrr package from tidyverse provides a more consistent and user-friendly set of map functions.

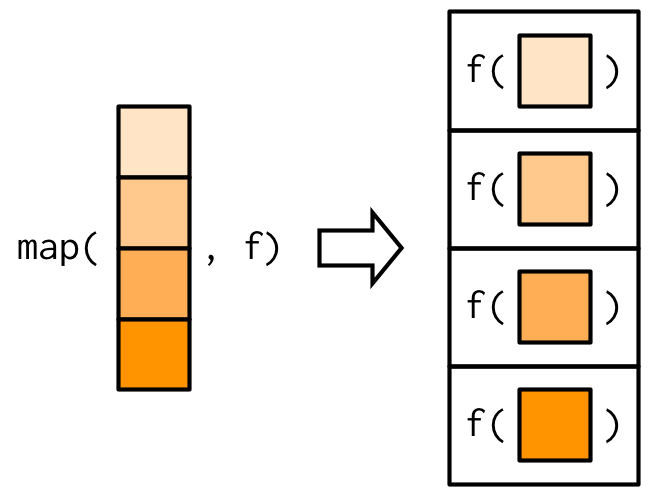
purrr::map

  • takes a vector and a function and calls the function once for each element of the vector;
  • returns a list;
  • implemented in C for performance.
library(purrr)
x <- c(1, 5, 7, 9)
f <- function(a) a^2
map(x, f)
[[1]]
[1] 1

[[2]]
[1] 25

[[3]]
[1] 49

[[4]]
[1] 81

is equivalent to list(f(x[1]), f(x[2]), f(x[3]), f(x[4])).

purrr::map

ADVR Ch. 9

purrr::map

returns an atomic vector…

  • map_lgl: of logicals
  • map_int: of integers
  • map_dbl: of doubles
  • map_chr: of characters

Inline (anonymous) functions

map(x, function(a) a^2)

purrr provide shortcuts for anonymous functions:

map(x, ~ .x^2)
map(1:5, ~ rnorm(n = 5, mean = .x))
[[1]]
[1] -0.3282237  0.7277602 -1.3256443  0.9296780 -0.2383811

[[2]]
[1] 2.079525 2.261968 4.012060 1.308766 2.579172

[[3]]
[1] 2.6821515 0.4448052 3.0792411 1.9976932 2.7107138

[[4]]
[1] 2.681011 4.252758 2.464766 5.616796 4.489707

[[5]]
[1] 4.439455 2.946883 4.587113 6.491458 4.724296

Additional arguments …

map(.x, .f, ..., .progress = FALSE)

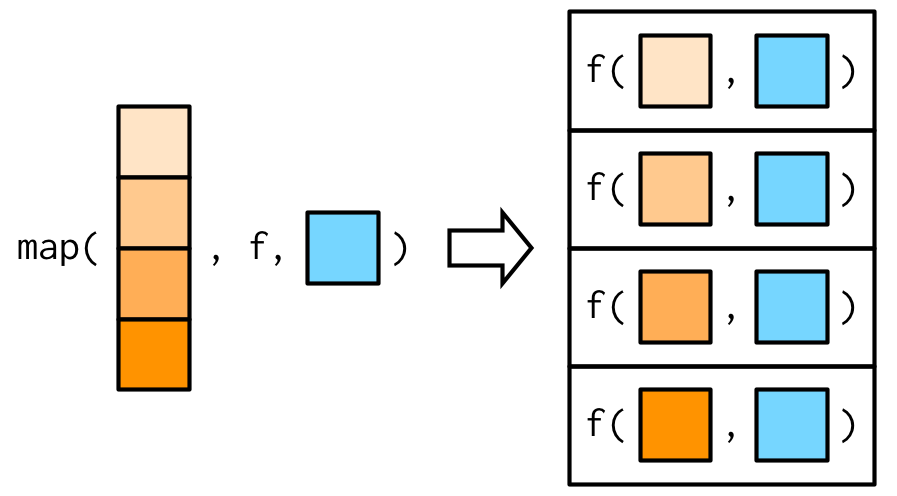
map will pass along any additional arguments (...) to the function .f.

map(1:5, function(n, m, s) rnorm(n, mean=m, sd=s), m = 10, s = 3)
[[1]]
[1] 6.700978

[[2]]
[1] 11.744477  2.494785

[[3]]
[1] 10.055895  8.362939  7.173781

[[4]]
[1]  6.753241 10.103854 10.489978 12.839883

[[5]]
[1]  8.643490 12.205973  9.802141  7.835962  9.243515

Additional arguments …

ADVR Ch. 9

Arguments do not get decomposed

ADVR Ch. 9

Quiz

map_dbl(1:5, `+`, runif(1))

vs

map_dbl(1:5, ~ `+`(.x, runif(1)))

Map variants

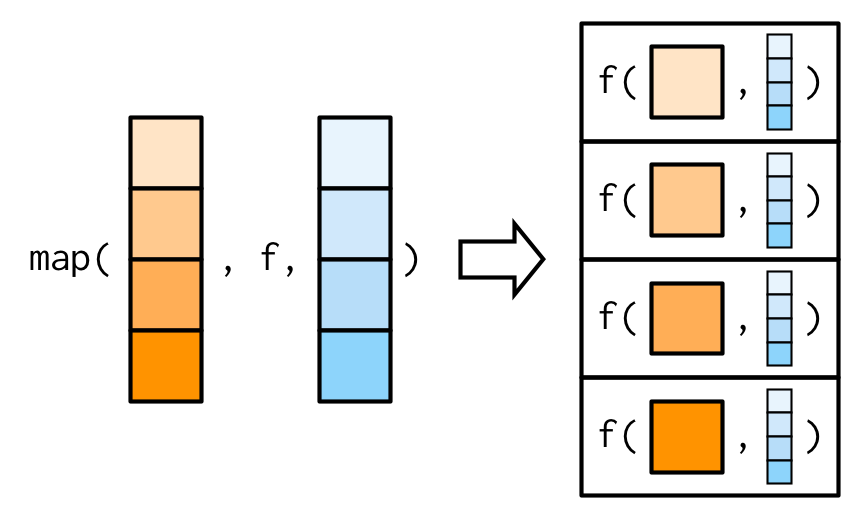
  • map2: iterate over two inputs.
  • pmap: iterate over multiple inputs.
  • imap: iterate with an index.

There’s also: - walk: no return value just walk through the input. - modify: output the same type as input.

walk and modify also have [walk|modify]2, p[walk|modify], and i[walk|modify].

Note: modify does not modify in place.

Quiz

map(mtcars, ~ .x * 2)

vs

modify(mtcars, ~ .x * 2)

walk

These functions are mainly for side-effects.

  • process the data and write to file via write.csv
  • create a plot and do ggsave

imap

imap can be seen as map2 with the second input being an index or name of the items in the first input.

xs <- c("apple"=1, "banana"=2, "kiwi"=3)
imap(xs, function(x, name) glue::glue("Name: {name}; Value: {x}"))
$apple
Name: apple; Value: 1

$banana
Name: banana; Value: 2

$kiwi
Name: kiwi; Value: 3
ys <- c(1, 2, 3)
imap(ys, function(x, i) glue::glue("Index: {i}; Value: {x}"))
[[1]]
Index: 1; Value: 1

[[2]]
Index: 2; Value: 2

[[3]]
Index: 3; Value: 3

Quiz

Replace imap call with map2.

ys <- c(1, 2, 3)
imap(ys, function(x, i) glue::glue("Index: {i}; Value: {x}"))

Quiz

Exercise 9.4.6 Q2 from ADVR.

Rewrite the following code to use iwalk() instead of walk2(). What are the advantages and disadvantages?

cyls <- split(mtcars, mtcars$cyl)
paths <- file.path(temp, paste0("cyl-", names(cyls), ".csv"))
walk2(cyls, paths, write.csv)

pmap

Ideal for working with data frames or lists of parameters.

params <- tibble::tribble(
  ~ n, ~ min, ~ max,
   1L,     0,     1,
   2L,    10,   100,
   3L,   100,  1000
)

pmap(params, runif)
[[1]]
[1] 0.2340386

[[2]]
[1] 81.52564 58.25198

[[3]]
[1] 136.9632 550.6070 642.7421

Note: column names match the argument names of runif.

pmap

params <- tibble::tribble(
~ a, ~ b, ~ c,
 1L,     0,     1,
 2L,    10,   100,
 3L,   100,  1000
)

pmap(params, function(a, b, c) runif(n = a, min = b, max = c))
[[1]]
[1] 0.06145762

[[2]]
[1] 17.82511 92.01756

[[3]]
[1] 136.7334 996.3097 272.6368

reduce

reduce(.x, .f, ..., .init, .dir = c("forward", "backward"))

reduce2(.x, .y, .f, ..., .init)
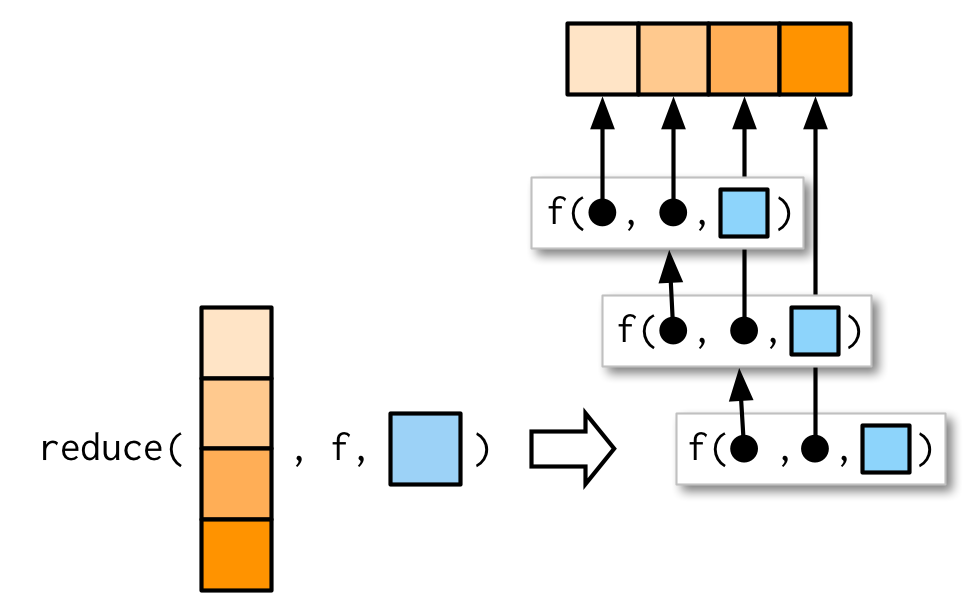
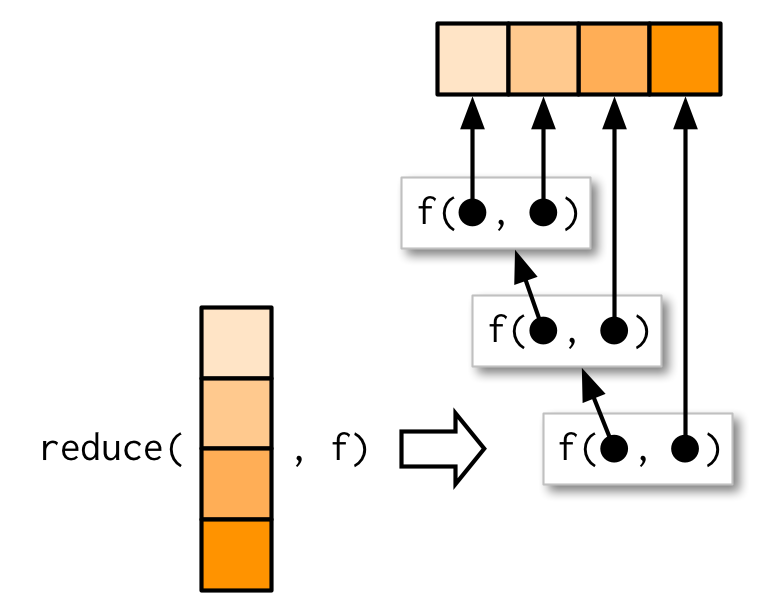
  • reduce(1:4, f) is equivalent to f(f(f(1, 2), 3), 4)
  • Generalise a function that works with two inputs (a binary function) to work with any number of inputs.
  • Result of the previous call to f is passed as the first argument to the next call to f.

reduce

ADVR Ch. 9

reduce

Write code to find intersection of a list of vectors.

x <- list(c(1, 3, 5), c(3, 5, 7), c(5, 7, 9))
intermediate_result <- intersect(x[[1]], x[[2]])
final_result <- intersect(intermediate_result, x[[3]])
print(final_result)
[1] 5

reduce

x <- list(c(1, 3, 5), c(3, 5, 7), c(5, 7, 9))
reduce(x, intersect)
[1] 5

reduce with arguments

ADVR Ch. 9

accumulate

A variant of reduce that returns the intermediate results as well.

x <- list(c(1, 3, 5), c(3, 5, 7), c(5, 7, 9))
accumulate(x, intersect)
[[1]]
[1] 1 3 5

[[2]]
[1] 3 5

[[3]]
[1] 5

Cumulative sum

Count the number of times a specific string appears in a corpus.

corpus <- c("the cat sat on the mat", "the dog sat on the log", "the cat chased the dog that sat on the couch.")
target <- "sat"
map(corpus, function(text, str_to_match) stringr::str_count(text, str_to_match), str_to_match=target) %>% 
  accumulate(`+`, .init = 0)
[1] 0 1 2 3

Quiz

Practice using map2_dbl and accumulate.

set.seed(123)
n <- 100
m <- 10
weights <- runif(n)
wbar <- weights / sum(weights)
values <- rnorm(n)
values[sample(x = n, size = m)] <- NA
# YOUR CODE: compute the weighted mean of values using accumulate and map2_dbl.

Predicate functionals

  • every: all elements satisfy a condition.
  • some: at least one element satisfies a condition.
  • detect: return the first element that satisfies a condition.
  • detect_index: return the index of the first element that satisfies a condition.
  • none: no elements satisfy a condition.
  • keep: keep elements that satisfy a condition.
  • discard: discard elements that satisfy a condition.
  • modify_if: modify elements that satisfy a condition.

Function factories

Function factories are functions that make functions.

The enclosing environment of the manufactured function is an execution environment of the function factory.

Function factories: environment

make_power <- function(n) {
  function(x) {
    x ^ n
  }
}
square <- make_power(2)
rlang::env_print(square)
<environment: 0x7f7dd44570f0>
Parent: <environment: global>
Bindings:
• n: <lazy>

It has binding to value n, which was passed in as an argument to make_power.

Function factories: lazy evaluation

What does n: <lazy> mean?

x <- 2
square <- make_power(x)
x <- 3
square(2)
[1] 8

What???

Function factories: lazy evaluation

The value of n is looked up when the function is called, not when it is created.

So if it was assigned to a variable in a parent environment (in this case, global) and that variable’s value is changed, the function will use the new value.

rlang::fn_env(square)$n
[1] 3

Function factories: force evaluation

make_power <- function(n) {
  force(n)
  function(x) {
    x ^ n
  }
}

x <- 2
square <- make_power(x)
x <- 3
square(2)
[1] 4

ggplot2: adjusting bin width

library(ggplot2)
sd <- c(1, 5, 15)
n <- 100

df <- data.frame(x = rnorm(3 * n, sd = sd), sd = rep(sd, n))

ggplot(df, aes(x)) + 
  geom_histogram(binwidth = 2) + 
  facet_wrap(~ sd, scales = "free_x") + 
  labs(x = NULL)

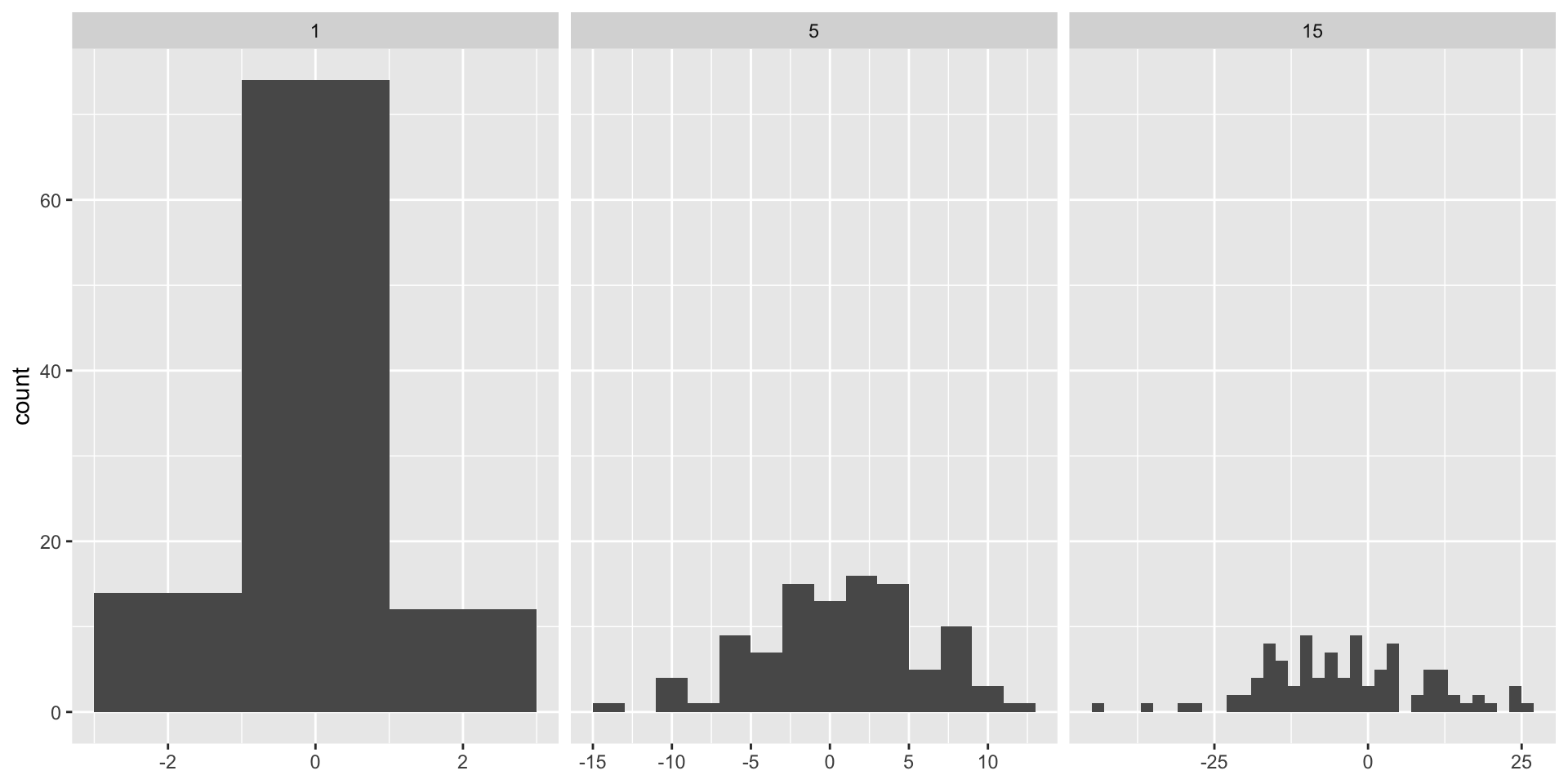
ggplot2: adjusting bin width

Roughly speaking, we want similar number of observations in each bin. In this case, variability in the data should be used to determine the bin width for each group.

binwidth: The width of the bins. Can be specified as a numeric value or as a function that calculates width from unscaled x. Here, “unscaled x” refers to the original x values in the data, before application of any scale transformation. When specifying a function along with a grouping structure, the function will be called once per group.

ggplot2: adjusting bin width

binwidth_bins <- function(n) {
  force(n)
  
  function(x) {
    (max(x) - min(x)) / n # divide the data range into n bins
  }
}

ggplot(df, aes(x)) + 
  geom_histogram(binwidth = binwidth_bins(20)) + # 20 bins
  facet_wrap(~ sd, scales = "free_x") + 
  labs(x = NULL)

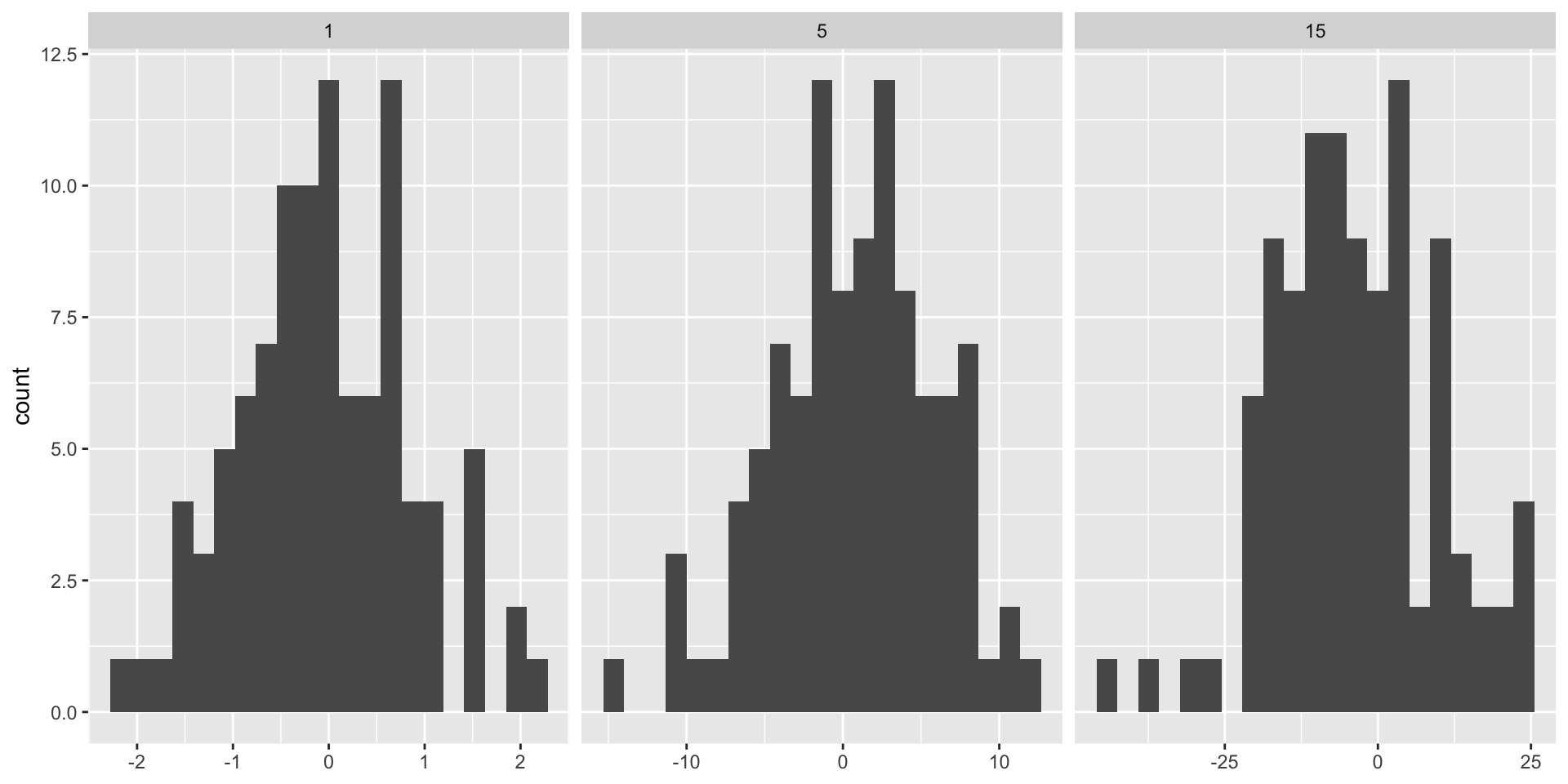
ggplot2: adjusting bin width

library(dplyr)
f <- binwidth_bins(20)
df %>% 
  group_by(sd) %>% 
  select(x) %>% 
  summarise(binwidth = f(x))
# A tibble: 3 × 2
     sd binwidth
  <dbl>    <dbl>
1     1    0.217
2     5    1.33 
3    15    3.40
  • n=20 indicates the total number of bins you want to divide the data into.
  • The binwidth is larger for large standard deviation.

Function factories and functionals

names <- list(
  square = 2, 
  cube = 3, 
  root = 1/2, 
  cuberoot = 1/3, 
  reciprocal = -1
)
funs <- purrr::map(names, make_power)
funs$root(9)
[1] 3
rlang::fn_env(funs$root)$n
[1] 0.5
rlang::fn_env(funs$cube)$n
[1] 3

Memoisation

  • A technique to cache the results of function calls.
  • Useful for functions that are computationally expensive and are called repeatedly with the same arguments.
fib <- function(n) {
  if (n <= 1) {
    return(n)
  }
  fib(n - 1) + fib(n - 2)
}
system.time(fib(30))
   user  system elapsed 
  1.531   0.016   1.560

Memoisation

library(memoise)
memoised_fib <- memoise(fib)
system.time(memoised_fib(30))
   user  system elapsed 
  1.500   0.009   1.514 
# Run it again!
system.time(memoised_fib(30))
   user  system elapsed 
  0.019   0.000   0.019

The values of fibonacci sequences for \(n \leq 30\) are cached after the first call, so subsequent calls are much faster.

Reference

  • Ch. 9-11 of Advanced R (2e) by Hadley Wickham and Jennifer Bryan.